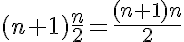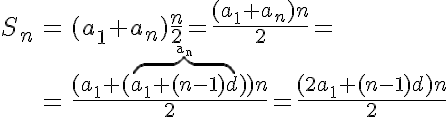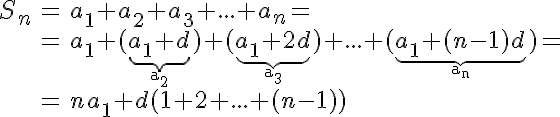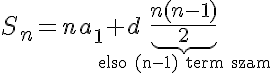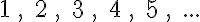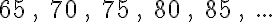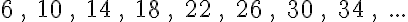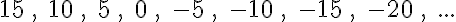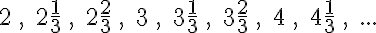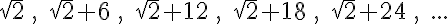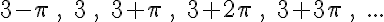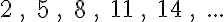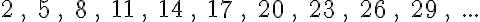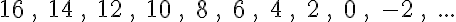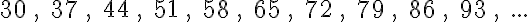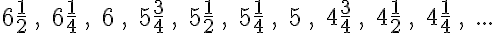matekérettség

A szöveges feladatok az érettségin (meg úgy általában a középiskolai matematikában) eröltetettek. Mindig arra kíváncsiak, hogy képes vagy-e megtalálni egy olyan helyzet mögött a matematikai struktúrát, ahol nem adják azt a kezedbe. Az itt következő feladatoknak mind az a kulcsa, hogy észrevedd, hogy milyen számtani sorozat húzódik meg mögötte. Ha Ez ki tudod találni, és sikerül azonosítani az első elemet, meg a differenciát, akkor már nem érhet meglepetés.

1. feladat: Egy könyvszekrény nyolc polca közül a legfelsőn 35 könyv van, és minden további polcon 4-gyel több, mint a felette levőn. Hány könyv van ebben a könyvszekrényben?

Iskolapéldája az olyan feladatnak, amit egy rajzzal meg némi számológépnyomkorászással akkor is meg tud oldani az ember, ha soha nem hallott szántani sorozatokról, meg hozzájuk tartozó képletekről. Próbáld meg képlettel megoldani, utána "nyomkorászással" ellenőrizheted.

2. feladat: egy trapéz alakú tetőrész becserepezésekor 12 sorban helyezik el a cserepeket, a legalsó sorba 84 cserép kerül, minden következőbe 4-gyel kevesebb. Hány cserép kell a tetőrészhez?

Vedd észre, hogy a feladat megoldásához tulajdonképp nem kell tudni, hogy a trapéz az hogyan is néz ki. Ha tudod jó, ha nem, semmi baj.

3. feladat: Március elsején a nappal 11 óra 4 percig tart, április 30-án pedig 14 óra 24 percig. Milyen hosszú a nappal április 12-én, ha feltételezzük, hogy az egymást követő nappalok hossza ugyanannyival növekedik.

Tipp: Érdemes lesz a nappalok hosszát átszámolni percre.

4. feladat: Egy 2 m hosszúságú sálat akarunk kötni. Ha az első napon 18 cm-t, majd pedig minden nap az előző napinál 4 cm-rel hosszabb darabot kötünk, akkor hány nap alatt készül el a sál?

5. feladat: Timi érettségire készül. Az harmadik héten 10 oldalt haladt a tananyagban. Az első héttől kezdve megfigyelte, hogy minden héten fél oldallal többet tud haladni a tananyagban, mint az előzőn (egyre ügyesebb ugyanis). Összesen 22 hetet tudot készülni az érettségire. Az utolsó héten hány oldalt haladt Timi? Összesen hány oldalt haladt Timi? Hány oldalt haladt Timi az utolsó 4 hétben? 

6. feladat: Egy koncertre úgy érkeznek az emberek, hogy a nyitás percében 37 ember jön be és minden további percben 3-mal több, mint az előzőben. Mikor telik meg a 3000 férőhelyes küzdőtér?

Egy történettel kezdjük ezt a részt. Gaussról a matematika egyik legnagyobb alakjáról mesélik a következő legendát. A falusi iskolában, ahova Gauss járt, a tanító egyszer – hogy kis nyugtot nyerjen a diákjaitól – azt a feladatot adta fel a diákoknak, hogy adják össze 1-től 100-ig a számokat.

1 + 2 + 3 + … + 100

A kis Gauss egy percen belül jelentkezett, hogy a végeredmény 5050. A tantó nagyon elcsodálkozott, mert valóban ez a helyes végeredmény, de ennyire gyors még Gauss se lehet. Megkérdezte hogyan jutott az eredményre, mire Gauss a következőt mondta el. Észrevette, hogy

• ha az első és az utolsó számot adja össze, az 1 + 100 = 101.
• Ha a másodikat, és az utolsó előttit, akkor az 2 + 99 = 101, vagyis ugyanannyi.
• Ha a harmadikat, meg hátulról a harmadikat, akkor az 3 + 98 = 101.
• …

Világos, hogy ha így halad „előről egyenként” illetve „hátulról egyenként”, akkor minden ilyen páros összeg 101 lesz. Már csak azt kell kitalálni, hány ilyen 101-el egyenlő összeg-pár van 1 és 100 között. Könnyű látni, hogy pont 50, fele annyi, ahány számot adunk össze (100). Látható is, hogy az összeg-párok az 50 + 51 = 101 összegnél érnek össze.

1 + 2 + 3 + … + 50 + 51 + … + 98 + 99 + 100

Így a feladat kérdésére a válasz: 50·101 = 5050. A döbbent és büszke tanító reakciója erre az volt "Én már nem tudok neked mit tanítani." (Ilyenek ezek a tanbák. :)

1. feladat: a történet ötletét a következő összegek kiszámításához használd fel (megoldások a bejegyzés végén):

1 + 2 + 3 + … + 40

1 + 2 + 3 + … + 67

Az eddigiekből megfogalmazható az első n darab természetes szám összege (bármilyen pozitív egész legyen is az n). Ugyanazt a gondolatot követve, mint ami a Gauss-féle megoldásban szerepel azt mondhatjuk, hogy

• az első és az utolsó szám összege 1 + n.
• A második és az utolsó előtti szám összege 2 + (n – 1) = n + 1.
• A harmadik és hátulról a harmadik szám összege 3 + (n – 2) = n + 1.
• …

Összesen hány ilyen n + 1 nagyságú összeg-párt kell vennünk? Hát, n/2 darabot, a képletünk tehát az első n természetes szám összege

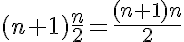
2. feladat: csavarjunk egyet az eddigieken! A Gauss-ötlet használható a következő összegek kiszámításánál is (megoldások a bejegyzés végén).

50 + 51 + 52 + … + 100 = ?

20 + 21 + 22 + … + 67 = ?

Ha maga az első n természetes szám összegére adott képlet nem is használható ezek kiszámításában, az ötlet ugyanúgy működik: első tag plusz utolsó tag, s az ilyen összegpárokból mindig fele annyi, ahány összeg-pár képezhető.

A módszer azért működik, mert hátulról „egyenként haladva visszafelé”, meg előről „egyenként haladva előrefelé” mindig eggyel csökken illetve eggyel nő az összeg.

3. feladat: lépjünk még egyet! A következő összegek kiszámításában is ugyanez az ötlet lesz a segítségünkre (megoldások a bejegyzés végén):

5 + 10 + 15 + 20 + … + 85 + 90 + 95 + 100 = ?

3 + 6 + 9 + 12 + 15 + … + 51 + 54 + 57 + 60 = ?

20 + 24 + 28 + 32 + … + 52 + 56 + 60 = ?

Ha jobban megnézzük, az utolsó feladatban odáig jutottunk, hogy tetszőleges számtani sorozat első n tagját össze tudjuk adni ezzel az ötlettel. (Ha esetleg nem sikerült megbírkózni vele, akkor most megfogalmazzuk a receptet és azzal már vissza lehet térni rá.) Gondoljuk ezt át! Vegyünk egy tetszőleges számtani sorozatot! Legyen ez mondjuk a következő:

6, 13, 20, 27, 34, …, 62, 69, 76, …

Adjuk össze ennek a sorozatnak a tagjait 76-ig! A sorozat első eleme a 6 (azaz a₁ = 6), a 76 a sorozat 11-edik eleme (a₁₁ = 76), a sorozat differenciája pedig 7 (d = 7). Az első és a 11-edik elem összege 6 + 76 = 82. A második és a tízedik elem összege 13 + 69 = 82, a harmadik és a kilencedik elem összege 20 + 62 = 82, és így tovább. Nem véletlen, hogy ez teljesül, hiszen az összeg-párok egyik tagja mindig a differenciával nő a másik pedig a differenciával csökken. A már megismert jelölésrendszerrel jelölve:

a₁ + a₁₁ = a₁ + (a₁ + 10d) = 2a₁ + 10d = 12 + 70 = 82

a₂ + a₁₀ = (a₁ + d) + (a₁ + 9d) = 2a₁ + 10d

a₃ + a₉ = (a₁ + 2d) + (a₁ + 8d) = 2a₁ + 10d

a₄ + a₈ = (a₁ + 3d) + (a₁ + 7d) = 2a₁ + 10d

…

Így a sorozat első 11 elemének az összege: (82 · 11) / 2 = 451.

Ha most az összegre adható általános képletet akarjuk kitalálni, akkor két úton is elindulhatunk.

1. út. A sorozat első n elemének összege az első és az utolsó elem összegéből álló összeg-pár összesen (n / 2)-ször. Azaz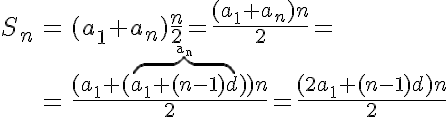

Itt látható, hogy egy sorozat első n elemének összegét a matematikában S_n-nel szoktuk jelölni, S₁₂ tehát egy sorozat első 12 elemének összegét jelöli (S₁₂ = a₁ + a₂ + ... + a₁₂).

2. út. Kiindulhatunk abból az összefüggésből is, amit az előző bejegyzésben kaptunk a számtani sorozat n-edik tagjára. (felhasználjuk az előző bejegyzésben levezetett képletet a számtani sorozat n-edik tagjára)

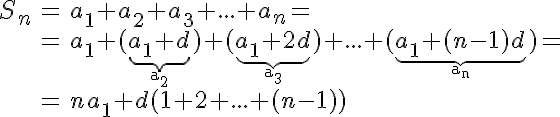
A d itt (1 + 2 + ... +(n-1))-gyel van megszorozva, ami az első (n-1) természetes szám összege, amit a bejegyzés elején adott képlettel tudunk számítani. Így végül a következőt kapjuk:

4. feladat: A két képlet nem azonos. Egyszerű átalakításokkal azonban az egyik a másikká alakítható. Keresd meg ezeket az átalakításokat. 

5. feladat: használd a képleteket (mindegy melyiket használod) a következő összegek megállapítására (megoldások a bejegyzés végén).

Mi a 3, 5, 7, 9, ... számtani sorozat első 130 elemének összege?

Mi a 8, 2, -4, -10, ... számtani sorozat első 36 elemének összege?

a₁ = 11, d = -1/2, S₂₄ = ?

a₁ = 300, d = 1/5, S₅₆ = ?

a₁ = 1, d = 17, S₄₀₀ = ?

a₈₁ = 213, d = 3, S₁₀₀ = ? (Tipp: itt nincs megadva az a₁ elem, de a d igen, és ennek ismeretében már tudjuk számítani az a₈₁-ből.)

Mi az első 30 darab 8-cal osztható természetes szám összege?  (Tipp: a feladat megoldása azon múlik, hogy meg tudod-e találni, hogy milyen számtani sorozatról van szó, azaz mi itt az a₁ és mi a d)

Mennyi a 6-tal osztható kétjegyű természetes számok összege? (Természetesen valójában ez a feladat is egy számtani sorozat összegére kérdez rá. Mondjuk itt az első elem kitalálásán túl az is kérdés, hogy hanyadik elem az utolsó elem.)

Mennyi a 3-al osztva 1 maradékot adó, legfeljebb kétjegyű természetes számok összege? (Fifikás feladat, megint azon múlik, hogy sikerül-e "visszakódolni", hogy milyen számtani sorozatra is kérdez rá.)

Megoldások:

1. feladat:

(1 + 40) · (40 / 2) = 41 · 20 = 820,

(1 + 67) · (67 / 2) = (68 · 67) / 2 = 2278.

2. feladat:

[(50 + 100) · 51] / 2 = 3825 (összesen 51 szám van 50 és 100 között az 50-et is beleszámolva! 1 és 100 között 100 szám van és ebből elhagyjuk az első 49-et. )

[(20 + 67) · 48] / 2 = 2088

3. feladat:

(105 · 20) / 2 = 1050

(63 · 20) / 2 = 630

(80 · 11) / 2 = 440

5. feladat:

130 · 3 + 2(130 · 129)/2 = 390 + (130 · 129) = 17160

8 ·36 + (-6) ·(36 · 35)/2 = 288 + (-3780) = -3492

24 · 11 + (-1/2)(24 · 23)/2 = 264 + (-138) = 126

300 · 56 + (1/5) · (56 · 55)/2 = 16800 + 308 = 17108

1 · 400 + 17 · (400 · 399)/2 = 400 + 1356600 = 1357000

a₁ = a₈₁ - 80d = 213 - (80 · 3) = 213 - 240 = -27. Így S₁₀₀ = -27 · 100 + 3 ·(100 · 99)/2 = -2700 + 7425 = 4725

a₁ = 8, d = 8, S₃₀ = 30 · 8 + 8 · (30 · 29)/2 = 240 + 3480 = 3720

a₁ = 12, d = 6, az utolsó elem 96 (a következő 6-tal osztható szám már háromjegyű). Hanyadik hattal osztható szám ez? Jobb híjján számológépnyomogatással is kitalálható. De pl. ebből is: 96/6 = 16, tehát ez a 16-ik hattal osztható természetes szám. Azaz a feladat S₁₆-ra kérdez rá, ami tehát 12 · 16 + 6(16 · 5)/2 = 192 + 240 = 432.

A legfeljebb kétjegyű természetes számok közül az első, ami hárommal osztva 1 maradékot ad az 1, tehát a₁ = 1. A következő ilyen természetes szám 3-mal nagyobb (4), az azutáni, megint 3-mal nagyobb (7), az azutáni megint (10) és így tovább.  Ebből adódik, hogy d = 3. A legutolsó olyan szám, ami legfeljebb kétjegyű és 3-mal osztva 1 maradékot ad a 97 (számológéppel kikeresgélhető). Hányszor kellett az első elemhez, az 1-hez 3-at adni, hogy 97 legyen? Összesen (97 - 1)/3 = 32-szer. Így tehát a 97 a sorozat 33-adik eleme, vagyis a feladat S₃₃-ra kérdez rá, ami 1 · 33 + 3(33 · 32)/2 = 33 + 1548 = 1617.

A számtani sorozatok igen sokfélék lehetnek. A következő sorozatok mind számtani sorozatok:

1. feladat: Ha alaposan megfigyeled, vajon meg tudod-e fogalmazni, hogy mi a közös ezekben a sorozatokban?

Próbálj meg válaszolni erre a kérdésre, mielőtt tovább olvasnál.

Megoldás: valami olyasmit vehetsz észre bennük, hogy ezek olyan sorozatok, ahol minden "lépésnél" ugyanannyival "növekszenek" a számok.

2. feladat: az itt felsorolt 7 sorozat esetében állapítsd meg, hogy melyik esetében mennyi ennek az állandónak az értéke, amivel "lépésenként növekednek" a számok! (Megoldások a bejegyzés végén)

Az első feladat megoldásának megfogalmazása elég pontatlan (emiatt a sok idézőjel), de a lényeget megragadja. A pontatlanságra szépen mutat rá a negyedik sorozat példája, ahol "növekedés" valójában csökkenés. Pontosabb a meghatározásunk, ha azt mondjuk, hogy

a számtani sorozat olyan számsorozat, amire az teljesül, hogy bármelyik két szomszédos elemének ugyanannyi a különbsége.

Ezt a különbséget idegen (latin) szóval differenciának szokták mondani, innen ered az, hogy a matematikában a számtani sorozatnak ezt az összetevőjét d-vel jelölik. A bejegyzés elején felsorolt sorozatok közül a harmadiknak a differenciája 4 (d = 4 mondaná a matematikus), az ötödiké pedig egyharmad (d = 1/3). A 2. feladat tulajdonképp ezeket a d értékeket kérdezi az összes sorozat esetében.

Az érettségin előforduló számtani sorozatos feladatok egy része azt igényli, hogy ki tudd találni, hogy egy adott számtani sorozatnak mi az n-edik eleme. Ilyen irányba haladunk most mi is a feladatokkal.

3. feladat: folytasd a következő számtani sorozatokat további 5 elemmel! (Megoldások a bejegyzés végén)

Tipp: az utolsó feladatnál segíthet ha felidézzük, hogy az 1/2 az 2/4.

Hogyan oldottad meg ezeket a feladatokat? Valószínűleg úgy, hogy először kitaláltad, hogy mi a sorozat differenciája (mondjuk az első két elem különbségéből), aztán ezt hozzáadtad az utolsó elemhez, majd az így kapott elemhez, majd az így kapott elemhez, stb.

Hogy kényelmesebb legyen hivatkozni ezekre az elemekre, a matematika azt a jelölést szokta használni, hogy a sorozat elemeit a₁, a₂, …, a_n,... jelekkel jelöli. Így a 3. feladat első sorozatában a₁ = 2, a₂ = 5, a₃ = 8, a₄ = 11, és a₅ = 14. Az előző bekezdésben elmondott "megoldási recept" most már precízebben megfogalmazható: először kitaláltad a d-t mondjuk az a₁ - a₂ kivonás segítségével, majd a₅ + d eredményeként megkaptad a₆-ot, a₆ + d eredményeként megkaptad a₇-et, és így tovább, általánosan:

a_n + d = a_n+1.

Tipp: ha a számológépeden két számot összeadsz, majd az = gombot sokszor megnyomod, akkor a számológép minden egyes újabb = nyomással újra hozzáadja a második számot a már megkapott összeghez. Ezzel tulajdonképp annak a számtani sornak az elemeit számolja ki, melynek első eleme az első szám, differenciája pedig a második szám. Ki is próbálhatod, hogy pl. a 2 + 3 = = = = = = = = = = ... gombnyomásokkal a 3. feladat első sorozatának elemeit kapod-e.

Világos, hogy innentől ha egy sorozatnak ismerjük az első elemét illetve a differenciáját (azaz a₁ és d adott), akkor akármelyik elemét ki tudjuk számolni. Az se fog ki rajtunk, ha esetleg nem az első eleme az adott. Ha pl. a₃ és d ismert egy sorozatból, akkor a₃-ból egyszer, illetve készer kivonva d-t megkapjuk a₂-t, illetve a₁-et ("visszafelé" haladunk a számsorban).

Ezzel végső soron kaptunk egy általános modszert egy számtani sorozat tetszőlegesen sokadik helyen álló elemének kiszámítására. (Ezt a "tetszőlegesen sokadik" kifejezést szokta úgy mondani a matematika, hogy n-edik.) Mégis sejthető, hogy számos esetben nem ez a "legtakarékosabb" megoldás. Tekintsük a következő feladatot:

4. feladat: mi a következő számtani sorozat századik eleme? 1, 2, 3, 4, 5, ...

Valószínűleg azonnal adtad rá a választ, hogy 100, holott ennek kiszámítása a fenti módszerrel még a számológép használata esetén is rengeteg gombnyomogatást igényelt volna.

5. feladat: ezekkel próbálj megmegbirkózni úgy, hogy egyelőre nem adom meg a pontos receptet a megoldásukra. Lehet, hogy megoldogatás közben megtalálod te magad is a receptet. Annak az a nagy értéke, hogy ha magad találod, arra mindig sokkal jobban fogsz emlékezni, mint ha csak bemagolod. A feladat után meg fogom adni a megoldási módot is, úgyhogy ha nem mennek nyugodtan olvass tovább, és majd visszatérhetsz a "recepttel" ezekhez a feladatokhoz.

• Mi a 2, 4, 6, 8, 10, ... számtani sorozat 60. eleme?
• Mi az 50, 55, 60, 65, 70, 75, ... számtani sorozat 18. eleme? 
• Mi a 0, 3, 6, 9, 12, ... számtani sorozat 50. eleme? 
• Mi a 10, 13, 16, 19, 22, ... számtani sorozat 50. eleme? 
• Mi a 6.15, 6.30, 6.45, 6.60, 6.75, 6.90, 7.05, ... számtani sorozat 1243. eleme?

Hogyan lehet megoldani ezeket a feladatokat? Természetesen az egyik lehetséges út a számológép hosszas pötyögtetése (ha másra nem ellenőrzésre sokszor igen jó). Ugyanakkor az utolsó feladat esetében semmiképpen nem időtakarékos megoldás. A megoldás, amire talán rá is jöttél, hogy nem kell egyenként elvégeznünk az "előre lépéseket" a számsorozatban. Ha a számsorozat két eleme között d a távolság, akkor 5d-t lépve 5 elemmel jutunk előrébb, 132d-t lépve pedig 132 elemet. Ha a számtani sorozat hetedik eleme a₇ = 12 és a differenciája d = 2, akkor nem csak az a₈-at tudjuk kiszámítani (ami nyilván 14), hanem az a₃₇-et is, hisz ahhoz 30-at kell "jobbra" lépni a sorozatban az a₇-től és minden lépés 2 nagyságú. Így összesen 30·2 = 60-nal nagyobb az a₃₇ az a₇-nél, vagyis a₃₇ = a₇ + 30·d = 12 + 60 = 72.

Ha általánosságban akarjuk megfogalmazni, akkor az a₁ és a d ismeretében például az a₈ = a₁ + 7d képlettel kapható meg, mert az a₈ összesen 7 "lépésnyire" van az a₁-től a sorozatban. Az általános n-edik elem képlete ugyanezen okból a_n = a₁ + (n - 1)·d.

Az 5. feladat kérdései ezzel a jelölésrendszerrel sokkal egyszerűbb formát öltenek, s a megválaszolásukhoz szükséges számítások is sokkal könnyebben áttekinthetővé válnak:

• a₁ = 2, d = 2, a₆₀ = ?
• a₁ = 50, d = 5, a₁₈ = ?
• a₁ = 0, d = 3, a₅₀ = ?
• a₁ = 10, d = 3, a₅₀ = ?
• a₁ = 6.15, d = 0.15, a₁₂₄₃ = ?

6. feladat: a 2. feladat után adtunk egy definíciót a számtani sorozat fogamára, de akkor még nem voltunk birtokában olyan jelöléseknek, mint d illetve a_n. Most, hogy már ismerjük ezeket a jelöléseket meg tudnád-e adni azt a feltételt, amit teljesítenie kell az a₁, a₂, …, a_n,... elemekből álló sorozatnak ahhoz, hogy számtani sorozat legyen?

Megoldások:

2. feladat: 1, 5, 6, -5, 1/3, 6, és

3. feladat: 

5. feladat: 120, 135, 147, 157, 192.45

6. feladat: hogy a_n+1 - a_n = d teljesüljön minden n-re.

Azt gondolom, hogy ezzel a témával (sorozatok) volna érdemes kezdeni. Amennyire látom az újfajta (már hogy számomra új) érettségiben mindig van olyan feladat, ami ebbe a témakörbe tartozik. Nem egy szuperbonyolult témakör, úgyhogy arra jó lesz, hogy elkezdjük vele kitapasztalni, hogy hogyan tudjuk ezt a blogolós, msn-ezős módszert használni.

Akkor belevágok...

A sorozatnak van precíz matematikai definíciója is, de erre nekünk egy középszintű érettségihez vajmi kevés szükségünk van, úgyhogy most a készüléshez elég lesz úgy gondolni a sorozat fogalmára, hogy az jó sok szám egymás után. A következők ezek szerint mind sorozatok:

6, 7, 8, 9, 10, ...

vagy

100, 200, 300, 400, 500, ... 

vagy

6, 0, -1, 6, 0, -1, 6, 0, -1, 6, 0, -1,...
vagy

3, 2, 1, 0, -1, -2, -3, -4, -5, ... 

vagy

1, 1000, 45, 2, 367, 1, 1, 456, ...

vagy

1, -1, 1, -1, 1, -1, 1, -1, ...

vagy

0.1, 0.3, 0.6, 0.4, 0.1, 0.1, 0.2, ...

és nyilván még rengeteget lehetne felírni.

Sorozatokra a való életben is lehet szép számmal példákat találni. Sorozatot kapunk, ha: 

• kiszámítjuk, és feljegyezzük minden nap az aznapi átlaghőmérsékletet,
• mégnézzük és feljegyezzük a tőzsdén a forint árfolymát minden nap délben,
• végigkövetjük egy internetes oldal látogatottságát napi bontásban,
• megmérjük vagy kiszámítjuk, hogy melyik nap milyen hosszú a nappal,
• felsoroljuk, hogy az osztályban kinek hanyasa van fizikából,
• felsoroljuk az atomok tömegét.

Természetesen ez a sor is folytatható tetszőleges hosszúságban. Azt gondolom, hogy léphetünk tovább.

A középiskolai matematika összesen kétféle sorozattal foglalkozik részletesebben. Az érettségihez nekünk is elég lesz, ha ezzel a kettővel ismerkedünk meg. Ezek: 

1. a számtani sorozat és
2. a mértani sorozat.

 Ezzel a kettővel kell nekünk is részletesebben foglalkoznunk.

Akkor elkezdjük!

Be kell valljam, roppant izgatott vagyok, hogy hogyan fog működni ez a dolog. Azóta, hogy megbeszéltük, hogy megpróbálkozunk ezzel a "távtanulással", vagy mivel, elég sokat gondolkodom azon, hogy hogyan is lehetne.

Ez a blog arra mindenképpen megfelel, hogy feladatsorokat rakjak össze neked, meg megmutassak általános megoldásokat. Ha valami nem megy, akkor máris van valami, amiről meg msn-en keresztül tudunk beszélgetni.

És akkor el is érkeztünk oda, amire egyelőre azt gondolom, hogy az egészből a legfontosabb: milyen stratégiával is tanuljunk?

1. Egyelőre nézzük meg, hogy tudod-e azt tartani, hogy minden nap 30 percet foglalkozol a matekkal. Ha ez megy, az nagyon jó (kurva jó - csak hogy örülj), akkor lényegében borítékolható, hogy meglesz az érettségi. Ha úgy látjuk, hogy nem megy, a napi 30 perc, akkor majd gondolkodunk, hogy mi megy.

2. Ha bármelyik feladat nem megy, akkor némi kis gyakorlatozás után tedd félre. Semmiképpen nem érdekünk, hogy felhúzd magad akár csak egy példa kapcsán is. Hogy meddig "erölködj" vele, arra az a javaslatom, hogy addig, amíg még van kedved küzdeni a példával. Ha nincs nyugodtan hagyd abba. Tedd félre. Vagy menj át másik példára, vagy hagyd a francba a matekot aznapra, és tanulj olyat, ami sikerélményt ad, esetleg csinálj valami teljesen mást (pl. rántotta:).

3. Ha egy példa nem ment, akkor később annyit tegyél meg vele, hogy próbáld meg magadnak pontosan megfogalmazni, hogy mi a baj a példával. Nyugodtan lehet az is a megfogalmazás, hogy "egy kurva nagy homály az egész". Az esetek többsgében mégis azt tippelem, hogy nem az lesz a helyzet, hogy egyáltalán semmi de semmi nem világos belőle. Sokszor ha pontosan meg tudod fogalmazni, hogy miért nem megy, akkor már félig meg is oldottuk a feladatot. És akkor nyilván ezekkel a feldatokkal foglalkozunk "élőben" msn-en.

4. Én se tudom még se azt, hogy pontosan mit hogyan kell így neten keresztül csinálni, se azt, hogy pontosan miben kell támasztani téged és miben vagy magadtól is erős. Egy pár már azért kiderült (pl. igen kitartó tudsz lenni, és ez nagy segítség, ugyanakkor ha jól sejtem, a  kudarcélmény nagyon elkeserít, meg eleve van egy olyan gondolat a fejedben, hogy neked ez úgyse megy), csak tisztában vagyok vele, hogy sok még menet közben fog. Ez azt jelenti, hogy most kísérletezzük ki együtt azt is, hogy mit érdemes, meg hogy hogyan érdemes. Egyrészt lehet, hogy menet közben változtatunk ezen-azon, másrészt nagyon fontos, hogy jelezzed majd menet közben, hogy mi az ami működik és mi az, ami nem.