A számtani sorozatok igen sokfélék lehetnek. A következő sorozatok mind számtani sorozatok:

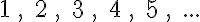
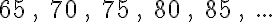
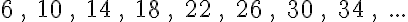
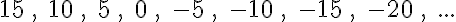
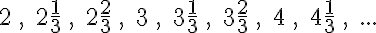
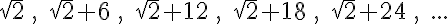
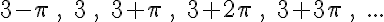
1. feladat: Ha alaposan megfigyeled, vajon meg tudod-e fogalmazni, hogy mi a közös ezekben a sorozatokban?

Próbálj meg válaszolni erre a kérdésre, mielőtt tovább olvasnál.

Megoldás: valami olyasmit vehetsz észre bennük, hogy ezek olyan sorozatok, ahol minden "lépésnél" ugyanannyival "növekszenek" a számok.

2. feladat: az itt felsorolt 7 sorozat esetében állapítsd meg, hogy melyik esetében mennyi ennek az állandónak az értéke, amivel "lépésenként növekednek" a számok! (Megoldások a bejegyzés végén)

Az első feladat megoldásának megfogalmazása elég pontatlan (emiatt a sok idézőjel), de a lényeget megragadja. A pontatlanságra szépen mutat rá a negyedik sorozat példája, ahol "növekedés" valójában csökkenés. Pontosabb a meghatározásunk, ha azt mondjuk, hogy

a számtani sorozat olyan számsorozat, amire az teljesül, hogy bármelyik két szomszédos elemének ugyanannyi a különbsége.

Ezt a különbséget idegen (latin) szóval differenciának szokták mondani, innen ered az, hogy a matematikában a számtani sorozatnak ezt az összetevőjét d-vel jelölik. A bejegyzés elején felsorolt sorozatok közül a harmadiknak a differenciája 4 (d = 4 mondaná a matematikus), az ötödiké pedig egyharmad (d = 1/3). A 2. feladat tulajdonképp ezeket a d értékeket kérdezi az összes sorozat esetében.

Az érettségin előforduló számtani sorozatos feladatok egy része azt igényli, hogy ki tudd találni, hogy egy adott számtani sorozatnak mi az n-edik eleme. Ilyen irányba haladunk most mi is a feladatokkal.

3. feladat: folytasd a következő számtani sorozatokat további 5 elemmel! (Megoldások a bejegyzés végén)

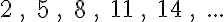
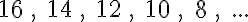
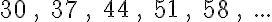
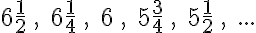
Tipp: az utolsó feladatnál segíthet ha felidézzük, hogy az 1/2 az 2/4.

Hogyan oldottad meg ezeket a feladatokat? Valószínűleg úgy, hogy először kitaláltad, hogy mi a sorozat differenciája (mondjuk az első két elem különbségéből), aztán ezt hozzáadtad az utolsó elemhez, majd az így kapott elemhez, majd az így kapott elemhez, stb.

Hogy kényelmesebb legyen hivatkozni ezekre az elemekre, a matematika azt a jelölést szokta használni, hogy a sorozat elemeit a₁, a₂, …, a_n,... jelekkel jelöli. Így a 3. feladat első sorozatában a₁ = 2, a₂ = 5, a₃ = 8, a₄ = 11, és a₅ = 14. Az előző bekezdésben elmondott "megoldási recept" most már precízebben megfogalmazható: először kitaláltad a d-t mondjuk az a₁ - a₂ kivonás segítségével, majd a₅ + d eredményeként megkaptad a₆-ot, a₆ + d eredményeként megkaptad a₇-et, és így tovább, általánosan:

a_n + d = a_n+1.

Tipp: ha a számológépeden két számot összeadsz, majd az = gombot sokszor megnyomod, akkor a számológép minden egyes újabb = nyomással újra hozzáadja a második számot a már megkapott összeghez. Ezzel tulajdonképp annak a számtani sornak az elemeit számolja ki, melynek első eleme az első szám, differenciája pedig a második szám. Ki is próbálhatod, hogy pl. a 2 + 3 = = = = = = = = = = ... gombnyomásokkal a 3. feladat első sorozatának elemeit kapod-e.

Világos, hogy innentől ha egy sorozatnak ismerjük az első elemét illetve a differenciáját (azaz a₁ és d adott), akkor akármelyik elemét ki tudjuk számolni. Az se fog ki rajtunk, ha esetleg nem az első eleme az adott. Ha pl. a₃ és d ismert egy sorozatból, akkor a₃-ból egyszer, illetve készer kivonva d-t megkapjuk a₂-t, illetve a₁-et ("visszafelé" haladunk a számsorban).

Ezzel végső soron kaptunk egy általános modszert egy számtani sorozat tetszőlegesen sokadik helyen álló elemének kiszámítására. (Ezt a "tetszőlegesen sokadik" kifejezést szokta úgy mondani a matematika, hogy n-edik.) Mégis sejthető, hogy számos esetben nem ez a "legtakarékosabb" megoldás. Tekintsük a következő feladatot:

4. feladat: mi a következő számtani sorozat századik eleme? 1, 2, 3, 4, 5, ...

Valószínűleg azonnal adtad rá a választ, hogy 100, holott ennek kiszámítása a fenti módszerrel még a számológép használata esetén is rengeteg gombnyomogatást igényelt volna.

5. feladat: ezekkel próbálj megmegbirkózni úgy, hogy egyelőre nem adom meg a pontos receptet a megoldásukra. Lehet, hogy megoldogatás közben megtalálod te magad is a receptet. Annak az a nagy értéke, hogy ha magad találod, arra mindig sokkal jobban fogsz emlékezni, mint ha csak bemagolod. A feladat után meg fogom adni a megoldási módot is, úgyhogy ha nem mennek nyugodtan olvass tovább, és majd visszatérhetsz a "recepttel" ezekhez a feladatokhoz.

• Mi a 2, 4, 6, 8, 10, ... számtani sorozat 60. eleme?
• Mi az 50, 55, 60, 65, 70, 75, ... számtani sorozat 18. eleme? 
• Mi a 0, 3, 6, 9, 12, ... számtani sorozat 50. eleme? 
• Mi a 10, 13, 16, 19, 22, ... számtani sorozat 50. eleme? 
• Mi a 6.15, 6.30, 6.45, 6.60, 6.75, 6.90, 7.05, ... számtani sorozat 1243. eleme?

Hogyan lehet megoldani ezeket a feladatokat? Természetesen az egyik lehetséges út a számológép hosszas pötyögtetése (ha másra nem ellenőrzésre sokszor igen jó). Ugyanakkor az utolsó feladat esetében semmiképpen nem időtakarékos megoldás. A megoldás, amire talán rá is jöttél, hogy nem kell egyenként elvégeznünk az "előre lépéseket" a számsorozatban. Ha a számsorozat két eleme között d a távolság, akkor 5d-t lépve 5 elemmel jutunk előrébb, 132d-t lépve pedig 132 elemet. Ha a számtani sorozat hetedik eleme a₇ = 12 és a differenciája d = 2, akkor nem csak az a₈-at tudjuk kiszámítani (ami nyilván 14), hanem az a₃₇-et is, hisz ahhoz 30-at kell "jobbra" lépni a sorozatban az a₇-től és minden lépés 2 nagyságú. Így összesen 30·2 = 60-nal nagyobb az a₃₇ az a₇-nél, vagyis a₃₇ = a₇ + 30·d = 12 + 60 = 72.

Ha általánosságban akarjuk megfogalmazni, akkor az a₁ és a d ismeretében például az a₈ = a₁ + 7d képlettel kapható meg, mert az a₈ összesen 7 "lépésnyire" van az a₁-től a sorozatban. Az általános n-edik elem képlete ugyanezen okból a_n = a₁ + (n - 1)·d.

Az 5. feladat kérdései ezzel a jelölésrendszerrel sokkal egyszerűbb formát öltenek, s a megválaszolásukhoz szükséges számítások is sokkal könnyebben áttekinthetővé válnak:

• a₁ = 2, d = 2, a₆₀ = ?
• a₁ = 50, d = 5, a₁₈ = ?
• a₁ = 0, d = 3, a₅₀ = ?
• a₁ = 10, d = 3, a₅₀ = ?
• a₁ = 6.15, d = 0.15, a₁₂₄₃ = ?

6. feladat: a 2. feladat után adtunk egy definíciót a számtani sorozat fogamára, de akkor még nem voltunk birtokában olyan jelöléseknek, mint d illetve a_n. Most, hogy már ismerjük ezeket a jelöléseket meg tudnád-e adni azt a feltételt, amit teljesítenie kell az a₁, a₂, …, a_n,... elemekből álló sorozatnak ahhoz, hogy számtani sorozat legyen?

Megoldások:

2. feladat: 1, 5, 6, -5, 1/3, 6, és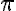

3. feladat: 

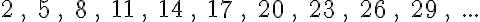
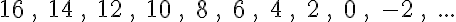
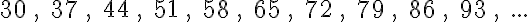
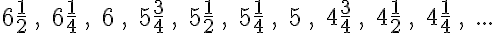
5. feladat: 120, 135, 147, 157, 192.45

6. feladat: hogy a_n+1 - a_n = d teljesüljön minden n-re.